科学研究

（通讯员/王艳成）近日👰🏻‍♀️，我院物理化学科教平台王艳成副教授与合作者在量子相变的无序算符标度行为研究中取得重要进展，在国际上首先提出利用无序算符来探测边界态和边界的临界行为，并分析了其标度行为。

5月17日，该成果以“Measuring the boundary gapless state and boundary criticality via disorder operator”为题，发表于国际著名物理刊物《物理评论快报》 Physical Review Letters 132🧟‍♂️， 206502 （2024）👨‍🎨，并获得编辑推荐（Editor’s suggestion）。审稿人对这项研究给予了高度评价💜，认为该项工作首次进行了表面临界的非局域物理量的测量尝试，并且给出了边缘模式与体内模式的耦合形式，对表面临界研究将有重要的指导作用➙，为理解表面临界行为提供了新的工具和视角。

论文原文链接🧑‍🤝‍🧑：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.206502

博士生刘泽楠为第一作者，王艳成副教授、西湖大学严正特聘研究员、中山大学姚道新教授为共同通讯作者🏄🏿，比利时根特大学黄瑞珍博士参与了理论工作🤰🏿。该项工作获得了浙江省自然科学基金重点项目⚰️、杏盛科研启动基金项目以及高性能计算中心的大力支持。

推动凝聚态物理学科乃至整个物理学科发展的一个巨大动力在于人们对新物态的不断探索及对相应新材料的制备、表征与应用🐺。在上个世纪的大部分时间里，人们对物态的认识和理解主要基于传统的朗道-金兹堡-威尔逊相变理论🐒👦🏽。据此理论，不同的物相由不同的局域序参量来刻画🤾，不同的序参量对应不同的对称性破缺🫷🏿。然而，随着二维KT相变理论的提出🤰🏼、强磁场下二维电子气中的整数与分数量子霍尔效应、拓扑绝缘体、量子自旋液体🚵🏻‍♀️🤾‍♂️、解禁闭量子临界点等新奇量子态以及与之相关的奇异量子相变的发现🏅，人们逐渐意识到传统的朗道-金兹堡-威尔逊理论框架已经不足以描述复杂的量子多体系统🛖，需要构建一套全新理论和相应物理量来刻画众多新奇的量子态和量子相变。

近年来，以无序算符为代表的非局域观测量的研究逐渐兴起，人们尝试从更高形式对称(higher-form symmetry)理论或者具有更一般数学形式的范畴对称（categorical symmetry）理论去理解物相和相变。该理论背后的动机是尝试在一个统一的框架下🔄，同时把满足朗道-金兹堡-威尔逊范式的物质形态和超越该范式的新奇量子态进行完整地描述，尝试建立起一个更宽广而全新的理论体系。无序算符作为一种非局域观测量，它能够揭示相和相变点的高阶对称性以及共形场论信息🧕，从更新更广阔的视角理解物相和临界行为♜。例如，在前期的工作中，我们可以利用无序算符来刻画不同的相以及不同相之间的临界行为。更为重要的是🕺🏼，我们能够利用无序算符提取出临界点上的流中心荷CJ等普适类信息【Phys. Rev. B 104, L081109 (2021)】。进一步，我们还可以借助无序算符来刻画超越传统朗道理论框架的解禁闭量子临界行为【Scipost Phys. 13，123 (2022)】。

另一方面🧑🏻‍🦯‍➡️，晶格系统的表面由于其边界格点的晶格失配往往展现出比体内更加丰富的表面临界行为。尤其是边缘模与体临界涨落耦合在一起🫸🏻，边界会诱导出许多新奇的相变行为👮🏽‍♂️，因而表面临界吸引了许多研究者的关注。如何在多体计算中🤨，提取边界临界行为的信息，进一步验证和指导目前的边缘临界理论，比如边缘共形场理论（boundary CFT），是量子多体理论与计算领域中的重要研究课题🙅🏽‍♂️。

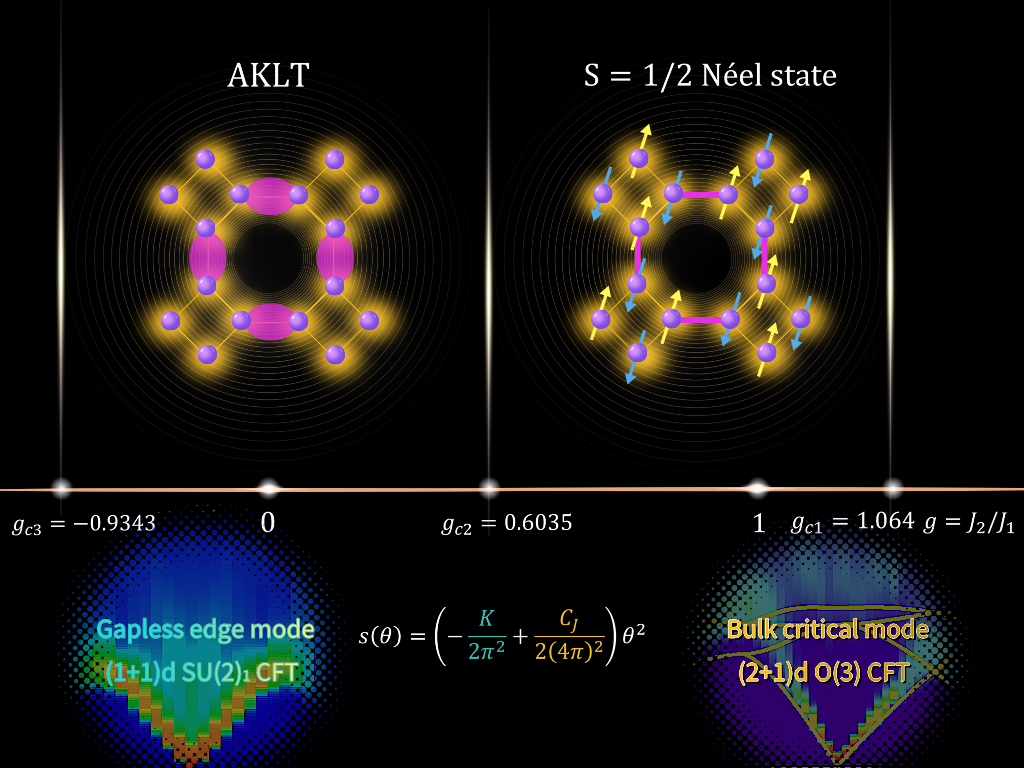
图1. S=1/2的AKLT模型的零温基态相图

无序算符的标度行为给出临界点处边缘模和体临界模耦合在一起的物理信息

王艳成副教授与合作者在前期对体临界无序算符标度行为的研究基础上，率先将无序算符用于对二维具有对称性保护拓扑相(symmetry protected topological phase, SPT)的AKLT模型的边界性质进行研究。在AKLT相中，边界的自旋形成有效的海森堡链。无序算符能够反映边缘态的物理性质，可以提取出海森堡链的拉廷哥液体（Luttinger liquid）参数，从而揭示(1+1)维边界SU(2)₁的物理🧜🏽‍♂️。当体系靠近相变点时🙆🏽‍♀️🗾，无能隙的边缘模与系统的体临界涨落逐渐耦合在一起，无序算符不但能够反映边缘态的(1+1)维的SU(2)₁物理🥷，还能够提取出体临界行为O(3)临界模的共形场论信息👨‍🦰。在此基础上😅🧛🏿‍♀️，对无序算符的标度行为提出了一个猜想🗄。在临界点处，无能隙边缘模和体临界模会以叠加的形式进入到无序算符的标度行为中👰🏻‍♀️，体现在其对数项中，它们遵从以下公式👳🏼：

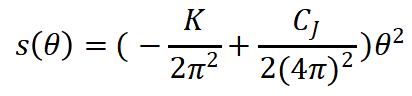
其中的K项由无能隙的边缘态提供，而CJ项由体的O(3)临界模贡献👩‍👧‍👧。我们的数值结果很好地验证了我们猜想👩🏼‍🚒。这也从数值角度直观揭示了边缘模与体临界涨落耦合的物理图像。

守正创新🚶🏻‍♀️，攻坚克难。仰望星空，脚踏实地🚣🏻。杏盛坚持科技创新引领发展，为实现高水平科技自立自强不懈奋斗！

（审核👳🏿：洪冠新 陈龙飞）

编辑🛅：谢雨倩 吴俊达